서랍원리 / 비둘기집의 원리(Pigeinhole principle) - 디리클레의 방 나누기

서랍원리 / 비둘기집의 원리 (Pigeinhole principle) - 디리클레의 방 나누기

불운의 아이콘 - 서랍원리

여기에 지지리 복도 없는, 하지만 머리는 좋은 친구 한 명이 있습니다.그래서 항상 손발이 고생하는...

 

어느 날 이 친구에게 아버지가 '안방에 들어가서 서랍에서 양말을 꺼내와'라고 하셨습니다.파란색, 빨간색 양말 아무거나 한 켤레 들고 와~그런데 운이 없는 이 친구, 안방에 전등이 나갔지 뭐예요? 양말 색깔이 도저히 구별이 안 가네요.파란색인지 빨간색인지...그놈이 이 놈 같고, 이 놈이 그 놈 같고...운이 없는 이 친구는 생각을 했습니다.난 운이 항상 없으니까 최소한 양말 몇 개를 꺼내면 반드시 같은 색의 양말이 있을까?

 

아무리 수학적이고 논리적으로 행동하더라도 운이 나쁜 경우에는 어쩔 수 없이 헛수고를 하게 됩니다.하지만 그러한 운이 나쁜 상황마저도 분석하여 헛수고를 최대 몇 번까지 해야 하는지, 운이 가장 나쁜 경우를 대비하는 방법이 무엇인지를 탐구하는 것이 수학의 놀라운 점입니다^^

 

위의 경우 만약 양말을 2개만 꺼낸다면 운이 좋은 경우에는 아래와 같은 결과가 나오겠지만,

운이 좋지 않은 경우에는 아래의 경우와 같이 짝이 맞지 않는 양말이 나오게 됩니다. 

결국 2짝을 꺼내는 경우에는 운이 좋지 않으면 같은 색 양말을 꺼낼 수가 없습니다.

1짝을 더 꺼내 볼까요?

모든 경우에 짝이 맞는 양말이 나온다는 것을 알 수 있습니다.

그러므로 적어도 3짝을 꺼내면 항상 짝이 맞는 양말이 생기게 됩니다.

 

이처럼 최악의 경우가 어떤 경우인지 알아내는 것은 '비둘기집의 원리'와 깊은 관계가 있습니다.

너무나 당연해 보이는 '비둘기집의 원리'가 의외로 많은 문제의 해법을 제공하듯이 최악의 경우를 알아내는 능력은 공학이나 실생활에서 큰 도움이 되기도 합니다.

 

비둘기집의 원리(Pigeinhole principle) - 디리클레의 방 나누기

독일의 수학자 중에 디리클레 (Dirichlet, 1805~1859)라는 사람이 있었습니다.

디리클레

디리클레는 우연히 지붕 위를 쳐다보게 되었는데 비둘기 세 마리가 정답게 놀고 있었습니다.

그런데 한 순간, 수학자 디리클레는 큰 걱정이 생겼습니다.

지붕에는 비둘기집이 두 개만 있었으므로 비둘기 한 마리의 잠자리가 걱정되었던 것입니다. 

"흠, 밤이 되면 한 마리 비둘기는 어디에서 잠을 자나? 비둘기집이 하나 부족하단 말이야."

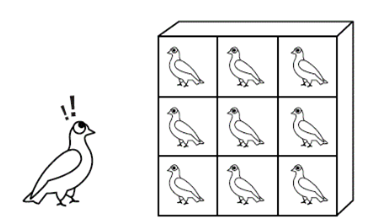
한동안 생각에 잠겼던 디리클레는 갑자기 얼굴이 밝아지더니 손으로 자신의 무릎을 쳤습니다. 

"맞다, 맞아. 비둘기 두 마리가 한 집에 자면 되겠어!"

이 정도의 생각으로 끝났다면 디리클레는 위대한 수학자가 될 수 없었을 것입니다.

수학자 디리클레는 비둘기의 수를 한 마리씩 늘리면서 이에 따라 비둘기집의 수도 늘려보았습니다.

그리고 수없이 반복해서 비둘기들이 비둘기집으로 들어가는 모든 가능성을 생각했고, 여기에서 아래와 같은 일반적인 공식을 만들어낸 것입니다.

 

(□+1)마리의 비둘기가 □개의 비둘기집에 들어간다고 할 때, 적어도 하나의 집에는 2마리 이상의 비둘기가 있습니다.

이 것이 그 유명한 '비둘기집의 원리'입니다.

 

서랍 원리와 비둘기집의 원리를 모두 다 알아봤습니다.

어떤가요? 서랍에선 꺼내고 비둘기집엔 넣고... 뭔가 비슷한 듯 다른 듯하죠? 

결국 둘은 똑같은 원리를 나타내고 있습니다.

서랍 속의 양말 색의 가짓수 = 비둘기집의 수

꺼내는 양말의 수 = 비둘기의 수

라고 생각하면 됩니다.

 

<비둘기집의 원리 적용식 Key point> 1. 어떤 조건을 비둘기집으로 볼 것인가? 몇 개인가? 2. 어떤 조건을 비둘기로 볼 것인가? 몇 개인가?

비둘기 집의 원리는 비록 교과과정에서는 다루지 않지만 수학 문제를 해결하는 데 있어서 중요한 사고방법 중의 하나입니다. 비둘기집의 원리는 누구나 쉽게 이해할 수 있을 만큼 쉬운 논리이지만 강력한 수학적인 원리로 수학의 여러 가지 분야에서 널리 쓰이고 있습니다. 

 

오늘은 비둘기 집 원리에 대해 알아보았습니다. 수학을 공부하는 가장 중요한 목적은 수학의 기본 지식을 활용하여 일상생활에서 일어나는 여러가지 문제를 해결하는 것입니다. 이 주제에서 다루게 되는 문장으로 표현된 생활 속의 수의 계산 문제가 바로 그런 문제라 할 수 있습니다. 이런 문제를 해결하는 과정에서 수학의 기초적인 개념, 원리, 법칙과 이들 사이의 관계를 터득하게 될 것입니다.